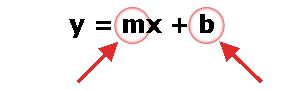miércoles, 27 de octubre de 2010
Elipse
| 6.2 LA ELIPSE | ||||
| Definiciones: i. Sean F y F’ dos puntos de un plano (F  . Se define la ELIPSE de focos F y F’ como el lugar geométrico de los puntos del plano tales que la suma de sus distancias a los focos es constante e igual a 2a (a > 0). ii. Las rectas: La que pasa por los focos F y F’ y la recta mediatriz del segmento  se llaman EJES DE SIMETRÍA DE LA ELIPSE. iii. El punto de intersección O de los dos ejes de simetría, se llama CENTRO DE LA ELIPSE. Los puntos A’, A, B y B’ se llaman VERTICES DE LA ELIPSE. Si el segmento  es mayor que el segmento  , ambos segmentos se llaman respectivamente EJE MAYOR y EJE MENOR de la elipse.
TEOREMA:
Demostración Si p(x, y) es un punto que pertenece a la elipse considerada, se tiene de acuerdo a la definición ique  , o equivalentemente, (fórmula de distancia entre dos puntos) Transponiendo el primer radical al segundo lado y elevando ambos miembros al cuadrado, se obtiene:  Simplificando la última igualdad se llega a:  Al elevar nuevamente ambos miembros al cuadrado en la última ecuación, se obtiene:  La cual se reduce a:  Recordando además que  y al dividir ambos miembros de la última igualdad por  , se obtiene finalmente  : que corresponde a la ecuación pedida. | ||||
y=x2
LA PARABOLA
Una función cuadrática es aquella que puede escribirse de la forma: f(x) = ax2 + bx + c, donde a, b y c son números reales cualesquiera y a distinto de cero. Si representamos "todos" los puntos (x,f(x)) de una función cuadrática, obtenemos siempre una curva llamada parábola.A continuación se muestran tres funciones cuadráticas con sus respectivas gráficas, de tres funciones cuadráticas muy sencillas:
a) f(x)= - x2 - 5x + 4 b) f(x)= - x2 - 5x + 4 c)f(x)= - 2x2 - 5x + 4
Para determinar el valor de las soluciones X1 y X2 respectivamente es necesario utilizar la siguiente formula:
Los valores correspondientes a , a, b y c, los desprendemos de la ecuación general de la forma: ax2 + bx + c = 0
Intersección de la parábola con los ejes.
a)-.Intersección con el eje Y: Como todos los puntos de este eje tienen la abscisa (eje x) x = 0, el punto de corte de la parábola con el eje Y tendrá de coordenadas (0,y).
b)-.Intersección con el eje X: Como todos los puntos del eje X tienen la ordenada (eje y) y = 0, para ver estos puntos de corte se resuelve la ecuación de segundo grado ax2 + bx + c = 0.
Dependiendo del valor del discriminante (D) de la ecuación, se pueden presentar tres situaciones distintas:
a-.Si D > 0, la ecuación tiene dos soluciones reales sean X1 y X2 y estas sean distintas y la parábola cortará al eje X en dos puntos.
b-.Si D = 0, la ecuación tiene una solución real es decir X1 = X2 y, por tanto, la parábola cortará al eje X en un punto (que será el vértice).
C-.Si D < 0, la ecuación no tiene soluciones reales y la parábola no cortará al eje X.
Vértice (V) de la parábola.
Corresponde al punto mínimo, cuando la curva es hacia abajo es decir a<0 y al punto máximo, cuando la curva es hacia arriba es decir a>0, en donde h será el punto del vértice en las absisas (eje x) y k será el punto del vértice en la ordenada (eje y).
Entonces: V (h, k)
h=-b/2a k=ah²+bh+c =( b²-2b²+4a)/4ª
http://www.youtube.com/watch?v=VucNU3Rk2nQ
y=mx+ b
Ecuación de una línea recta
VIDEO
http://www.youtube.com/watch?v=BPT_ZVohgVU
La ecuación GENERAL de una línea recta tiene la forma:
y = mx + b¿Qué significa?
 |
| |||||
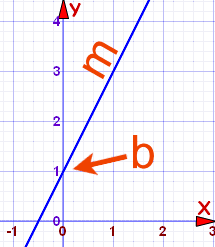
y = cuánto arriba x = cuán lejos m = gradiente o pendiente (cuán inclinada es la línea) b = la intersección Y (donde la línea se cruza con el eje Y) Las ecuaciones lineales son siempre de la forma: y = mx + b Donde m es la pendiente y la b es el intercepto en y. El intercepto en y esta expresada por: (0,b) y es donde la recta corta el eje de y El intercepto en x esta expresada por: (a,0) y es donde la recta corta el eje de x. Si la ecuación es y = 2x + -6, el intercepto en y seria: (0,-6) Ejemplo 1: Buscar el intercepto en y de la ecuación y = 3x + -5. Solucion: En este caso, la b es -5; quiere decir que el intercepto en y es (0, -5) Ejemplo 2: Buscar el intercepto en y de la ecuación y = 4x. Solucion: En este caso, la b no está presente en la ecuación, pero la ecuación y = 4x equivale a y = 4x + 0. Por lo tanto, el intercepto en y es (0, 0). Ejemplo 3: Buscar el intercepto en y de la ecuación 3y = 18x + 24 Solucion: ¡Ojo! El intercepto en y no es 24, hay que fijarse bien que la ecuación no esta en su forma y = mx + b, hay que despejar de la siguiente manera: 3y = 18x + 24 3 3 3 y = 6x + 8 < Ahora, esta en su forma y = mx + b. El intercepto en y es (0,8)> | ||||||
Suscribirse a:
Entradas (Atom)